
Atombau
1. Elementarteilchen im Atom
Materie setzt sich zusammen aus Atomen. Es hat sich als sehr zweckmäßig erwiesen, mit den Atomen als Bausteinen der Materie zu arbeiten, weil sich die Eigenschaften der Atome recht gut in einen Zusammenhang bringen lassen mit den Eigenschaften der Materie. Das allgemeine Wort Materie wird in der Chemie selten benutzt, der Chemiker spricht lieber von Stoffen, oder noch besser von Substanzen.
Eine Substanz besteht also aus Atomen. Man kann aber nicht sagen, daß Atome die kleinsten Teilchen einer Substanz sind, denn Atome sind selbst nicht kompakt und einheitlich, sondern sie sind ihrerseits wieder aus kleineren Teilchen zusammengesetzt, die man als Elementarteilchen bezeichnet.
Für die Bedürfnisse der Chemiker - und meist auch der Mediziner - reicht es aus, sich mit drei Elementarteilchen zu beschäftigen:
- Proton
- Neutron
- Elektron
Diese drei Elementarteilchen lassen sich durch ihre Masse und ihre elektrische Ladung charakterisieren.
1.1. Masse der Elementarteilchen
Proton und Neutron haben ungefähr die gleiche Masse. Das Elektron hat im Vergleich zu Proton und Neutron eine verschwindend kleine Masse.
Würde man die Masse der Elementarteilchen in der Einheit Gramm angeben, dann hätte man es mit sehr kleinen unhandlichen Zahlen zu tun, die man sich kaum merken könnte. Das Proton hätte dann z.B. die Masse 1.6725*10-24 g, das ist das gleiche wie 0,000 000 000 000 000 000 000 001 6275 g. Deshalb verwendet man im atomaren Bereich eine kleinere Einheit, die sogenannte Atommasseneinheit, abgekürzt AME oder u von atomic mass unit. Die genaue Definition dieser Masseneinheit wird hier nicht besprochen. Sie sollten sich merken:
Proton und Neutron haben ungefähr die Masse 1 AME. Das Elektron hat ungefähr die Masse 5*10-4 AME.
Die Massen der drei Elementarteilchen stehen zueinander also im Verhältnis:
Proton Neutron Elektron
1 : 1 : 5*10-4
Falls Sie die Massen der Elementarteilchen ganz genau wissen wollen:
Proton: 1.007276 AME
Neutron: 1.008665 AME
Elektron: 0.0005486 AME
1.2. Ladung der Elementarteilchen
Die drei Elementarteilchen Proton, Neutron und Elektron unterscheiden sich in ihrer elektrischen Ladung:
Das Proton ist einfach positiv geladen
Das Neutron ist elektrisch neutral.
Das Elektron ist einfach negativ geladen.
Proton und Elektron tragen jeweils eine elektrische Elementarladung. Der Begriff "elektrische Elementarladung" bedeutet, daß alle experimentell meßbaren Ladungen ganzzahlige Vielfache dieser Ladungsmenge sein müssen. Oder anders ausgedrückt: Man kann experimentell keine kleinere Ladungsmenge finden als die Elementarladung.
Das Proton trägt also die Ladung +1.
Das Neutron trägt die Ladung 0.
Das Elektron trägt die Ladung -1.
Die Daten der drei Elementarteilchen sind zur besseren Übersicht in Tabelle 1 zusammengestellt.
Tabelle 1: Masse und Ladung der Elementarteilchen
|
Elementarteilchen |
Masse ( abgerundet) |
Ladung |
|
Proton |
1 AME |
+1 |
|
Neutron |
1 AME |
0 |
|
Elektron |
5*10-4 AME |
-1 |
1.3. Verteilung der Elementarteilchen im Atom
Wie sind nun die Elementarteilchen Proton, Neutron und Elektron im Atom verteilt?
Ein Atom enthält im Zentrum einen kleinen Atomkern, der aus Protonen und Neutronen zusammengesetzt ist. Die Elektronen bilden um diesen Kern eine weite lockere Atomhülle.
Wenn man Ladung und Masse der Elementarteilchen betrachtet , läßt sich für Atomkern und Atomhülle folgern:
Der Atomkern muß positiv geladen sein, weil er außer den elektrischen neutralen Neutronen die positiv geladenen Protonen enthält.
Die Atomhülle muß negativ geladen sein, weil sie die negativ geladenen Elektronen enthält.
Der Atomkern enthält praktisch die gesamte Masse des Atoms, weil sowohl Neutron wie Proton um einen Faktor von etwa 5*104 schwerer sind als ein Elektron. Ein Atom, das z.B. aus 20 Protonen, 20 Neutronen und 20 Elektronen zusammengesetzt ist, hat einen Atomkern mit der Masse 40 AME und eine Atomhülle mit der masse 0.01 AME. Die Masse der Atomhülle macht in diesem Fall nur 0,025 % der Masse des Atomkerns aus.
Der Atomkern nimmt nur einen winzigen Bruchteil des Atomvolumens ein. Die Neutronen und Protonen sind im Atomkern sehr dicht gepackt, während die Elektronen eine sehr lockere Atomhülle bilden. Zur Veranschaulichung sollen einige Zahlen dienen:
Der Durchmesser eines Atoms ist von der Größenordnung 10-8 cm, während der Atomkern einen Durchmesser von nur etwa 10-13 cm hat, das heißt, er ist 100 000 mal kleiner. Hätte das Atom die Größe eines Fußballstadions, dann könnte man den Kern mit einem in der Mitte schwirrenden Insekt verleichen.
Um bei Längenangaben im atomaren Bereich nicht immer mit unhandlichen Zehnerpotenzen arbeiten zu müssen, gibt man Längen meist nicht in cm an, sondern in Ångström (Å).
1 Å = 10-8 cm.
Ein Atom hat in Ångström ausgedrückt einen Durchmesser von etwa 1 Å,
der Kern hat einen Duchmesser von etwa 10-5 oder 0.00001 Å.
2. Atomkern
Der Atomkern wird nicht ausführlich behandelt, weil für die Chemie die Elektronenhülle wichter ist. Hier sollen nur einige wichtige Begriffe besprochen werden.
2.1. Kernladungszahl
Der Atomkern ist immer positiv geladen. Die Zahl der positiven Ladungen im Kern wird bestimmt durch die Zahl der Protonen. Man bezeichnet diese Zahl als Kernladungszahl des Atoms.
2.2. Elementbegriff
Duch die Kernladungszahl läßt sich der Begriff Element eindeutig definieren:
Ein Element enthält ausschließlich Atome mit der gleichen Kernladungszahl d.h. mit der gleichen Anzahl von Protonen im Atomkern.
2.3. Ordnungszahl
Die Kernladungszahl kann als Kennziffer für ein Element dienen. Man kann die Elemente in der Reihenfolge dieser Kennziffer ordnen, deshalb wird die Kernladungszahl auch als Ordnungszahl bezeichnet.
Protonenzahl = Kernladungszahl = Ordnungszahl
Die Ordnungszahl 1 ist z.B. charakteristisch für das Element Wasserstoff, die Ordnungszahl 6 für das Element Kohlenstoff.
2.4. Massenzahl
Eine weiere Kennziffer für ein Atom ist die Massenzahl. Sie gibt die Summe von Protonen und Neutronen im Atomkern an.
Protonenzahl + Neutronenzahl = Massenzahl
Um Mißverständnissen vorzubeugen, sei betont, daß die Massenzahl nicht etwa die Masse des Atomkerns angibt, sondern nur die Anzahl der Teilchen. Die Massenzahl ist deshalb immer eine ganze Zahl. Da jedoch sowohl Protonen als auch Neutronen annähernd die Masse 1 AME haben, ist die Kernmasse, ausgedrückt in AME, der Massenzahl sehr ähnlich. Auf die Masse der Atome wird hier nicht eingegangen.
2.5. Isotope
Wie auf den vorhergehenden Texten besprochen, ist ein Element charakterisiert durch eine bestimmte Anzahl von Protonen im Atomkern. Dagegen können die Atome ein und desselben Elements verschieden viele Neutronen im Kern haben. Alle Atome eines Elements besitzen also die gleiche Kernladungs- oder Ordnungszahl, sie können sich aber unterscheiden in den Massenzahlen.
Man nennt solche Atome eines Elements, welche die gleiche Zahl von Protonen aber eine unterschiedliche Zahl von Neutronen besitzen, Isotope.
Isotope sind Atome mit gleicher Kernladungszahl, aber mit verschiedenen Massenzahlen.
Vom Element Chlor mit der Ordnungszahl 17 gibt es z.B. zwei Isotope; sie haben die Massenzahlen 35 und 37. Wieviele Neutronen haben diese Chlorisotope? 18 und 20.
Vom Element Wasserstoff mit der Ordnungszahl 1 gibt es drei Isotope; sie haben die Massenzahlen 1, 2 und 3. Diese drei Wasserstoffisotope haben ausnahmsweise auch verschiedene Namen: "Wasserstoff", "Deuterium", " Tritium". Das gewöhnlich als Wasserstoff bezeichnete in der Natur vorkommende Element enthält alle drei Isotope.
Die folgende Tabelle soll die Zusammensetzung des Atomkerns für die drei Wasserstoffisotope zeigen.
| "Wasserstoff" | "Deuterium" | "Tritium" | |
| Protonenzahl | 1 | 1 | 1 |
| Massenzahl | 1 | 2 | 3 |
| Neutronenzahl | 0 | 1 | 2 |

Die Elemente Wasserstoff und Chlor, die hier als Beispiele dienten, um den Begriff der Isotope zu erläutern, stellen keine Sonderfälle unter den Elementen dar. Nur wenige Elemente enthalten ausschließlich Atome mit der gleichen Massenzahl.
Die meisten Elemente bestehen aus einem Isotopengemisch.
Man nennt Elemente, von denen es jeweils nur ein Isotop gibt auch Reinelemente und Elemente mit mehreren Isotopen Mischelemente.
Das Element Natrium beispielsweise ist ein Reinelement, während die Elemente Chlor und Wasserstoff zu den Mischelementen gehören.
Im folgenden soll noch kurz auf die Häufigkeit der Isotope von Mischelementen eingegangen werden.
Das Element Chlor besteht zu 75.4 % aus dem Isotop mit der Massenzahl 35 und zu 24.6 % aus dem Isotop mit der Massenzahl 37. Jede beliebige Probe Chlor, ganz gleich welchen Ursprungs, weist dieses Isotopenverhältnis auf. Beim Wasserstoff macht das Isotop mit der Massenzahl 1 99.986 % aus, Deuterium ist mit 0.014 % enthalten und Tritium tritt nur in Spuren auf. Auch für dieses Element ist die Zusammensetzung weitgehend konstant, ganz gleich aus welchem Ausgangsmaterial man den Wasserstoff gewinnt.
Was hier für die Elemente Chlor und Wasserstoff dargelegt wurde, gilt allgemein für Mischelemente:
Bei Mischelementen ist die Zusammensetzung des Isotopengemisches weitgehend konstant.
Überall auf der Erde treten die einzelnen Isotope eines Mischelements praktisch mit der gleichen Häufigkeit auf.
2.6. Schreibweise
In der Chemie hat jedes Element sein eigenes Buchstabensymbol, z.B. steht für Wasserstoff H, für Chlor Cl, für Eisen Fe. Will man für ein Element genauere Angaben über den Atomkern machen, oder speziell von einem Isotop sprechen, dann schreibt man an das Elementsymbol links oben die Massenzahl und links unten die Ordnungszahl.
Für die drei Wasserstoffisotope würde man also schreiben:
1 2 3
H ( Wasserstoff) H (Deuterium) H (Tritium)
1 1 1
und für die beiden erwähnten Chlorisotope:
35 37
Cl und Cl
17 17
3. Elektronenhülle
Für die Chemie ist die Elektronenhülle der Atome viel wichtiger als der Atomkern, denn bei chemischen Reaktionen werden nur die Elektronen umgeordnet, der Kern bleibt unverändert. Die Struktur der Elektronenhülle bestimmt das Verhalten eines Elements bei chemischen Reaktionen; und die Vielfalt der chemischen Reaktionen wird überschaubarer, wenn man die Anordnung der Elektronen in der Atomhülle kennt.
Von den Elektronen der Atomhülle sind vor allem drei Dinge zu besprechen:
- Zahl
- Energie
- räumliche Anordnung
3.1. Zahl der Elektronen
Jedes Elektron trägt eine negative Ladung. Da ein Atom als Ganzes elektrisch neutral ist, muß die Zahl der Elektronen in der Atomhülle die positiven Ladungen des Kerns kompensieren. Daraus folgt:
Elektronenzahl = Protonenzahl = Kernladungszahl = Ordnungszahl
Jedes Element hat im Atomkern eine charakteristische Zahl von Protonen, es hat also auch in der Atomhülle die gleiche charakteristische Zahl von Elektronen.
Beispiele:
Wasserstoff (H): Kernladungszahl 1, Elektronenzahl 1
Kohlenstoff (C): Kernladungszahl 6, Elektronenzahl 6
3.2.Energie der Elektronen
3.2.1 Energie und Kernabstand
Ungleichnamige Ladungen ziehen sich an, ein negativ geladenes Elektron in der Umgebung des positiven geladenen Atomkerns hat also die Tendenz, der elektrischen Anziehungskraft des Kerns zu folgen und möglichst nahe an ihn heranzukommen. Will man ein Elektron, das sich sehr nahe beim Atomkern aufhält in eine größere Entfernung vom Kern bringen, muß man gegen die elektrische Anziehungskraft des Kerns Arbeit aufwenden. Durch diese Arbeitsleistung führt man dem Elektron einen bestimmten Energiebetrag zu, man vergrößert also damit die Energie des Elektrons.
Man muß einem Elektron Energie zuführen, um den Abstand zwischen Elektron und Atomkern zu vergrößern.
Die Energie eines Elektrons ist um so größer, je größer sein Abstand zum Kern ist.
3.2.2. Energieniveauschema
Anhand eines alltäglichen Beispiels sollen nun die Begriffe Energieniveau und Energienieveauschema eingeführt werden
Um einen auf dem Boden liegenden Stein entgegen der Schwerkraft auf einen Tisch zu heben, muß man ihm Energie zuführen. Der Stein auf dem Tisch ist energiereicher als der Stein auf dem Boden; das wird deutlich, wenn der Stein die gespeicherte Energie beim Herunterfallen etwa in Form von Wärme wieder abgibt.
Man kann auch sagen: Der Stein auf dem Tisch befindet sich in einem höheren Energiezustand als der Stein auf dem Boden.
Graphisch ist dieser Sachverhalt in einem sogenannten Energieniveauschema dargestellt:
Abb. 1
Der senkrechte Pfeil links in Abb. 1 stellt eine Energieskala dar, auf der aber keine Einheiten angegeben sind, weil in einem solchen Energieniveauschema meist nur qualitativ die relative Lage der Energieniveaus zueinander dargestellt werden soll. Durch den Pfeil wird lediglich angezeigt, daß die Energie in dem Diagramm nach oben zunimmt.
Die waagrechten Striche stellen die Energieniveaus dar; sie markieren auf der Energieskala jeweils die Energie, die der Stein enthält, wenn er auf dem Boden bzw. wenn er auf dem Tisch liegt. Das untere Energieniveau hat willkürlich die Nummer 1 erhalten und das obere Energieniveau die Nummer 2.
3.2.3. Elektronenschalen
Die Elektronen der Atomhülle haben nicht alle die gleiche Energie; sie verteilen sich vielmehr auf verschiedene Energieniveaus oder Energiezustände. In Abb. 2 sind in einem Energieniveauschema vier Energieniveaus der Elektronenhülle in ihrer relativen Lage zueinander dargestellt.
Die Energieniveaus der Abb. 2 sind sogenannte Energiehauptniveaus der Elektronenhülle; häufiger weden sie als Schalen bezeichnet. Der Begriff "Schale" stammt aus einer Zeit, als man noch andere Vorstellungen vom Atom hatte als heute, näher soll hier nicht darauf eingegangen werden.
Die Elektronen der Atomhülle sind auf Energiehauptniveaus oder Schalen mit unterschiedlicher Energie verteilt.
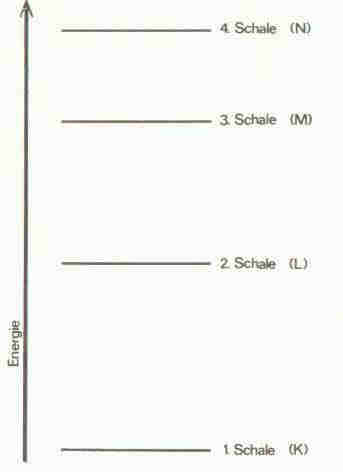 Abb.
2: Energieniveauschema für die vier untersten Elektronenschalen
Abb.
2: Energieniveauschema für die vier untersten Elektronenschalen
Wie Abb. 2 zeigt, werden die Elektronenschalen außer durch Nummer auch noch durch die Großbuchstaben K, L, M und N gekennzeichnet. In diesem Programm werden ausschließlich die Nummern verwendet.
Sie können dem Energieniveauschema von Abb. 2 folgende Informationen entnehmen:
Den niedrigsten Energieinhalt haben Elektronen, die sich in der 1. Schale befinden.
Um ein Elektron von der 1. Schale in die 2., 3. oder 4. Schale zu bringen, muß man ihm Energie zuführen.
Ein Elektron, das von der 2. Schale in die 1. Schale überwechselt, muß dabei Energie abgeben.
Die Engergiedifferenz zwischen je zwei benachbarten Schalen wird mit zunehmender Engerie der Schalen immer kleiner.
Außer den in Abb. 2 eingezeichneten vier Schalen gibt es noch energiereichere, die hier de Übersichtlichkeit wegen nicht eingetragen sind.
3.2.4. Energiequantelung
Im Abschnitt 3.2.3 sind die Elektronenschalen der Atomhülle vorgestellt worden als Energieniveaus, auf die sich die Elektronen verteilen. Dazu muß noch ergänzend gesagt werden: Ein Elektron in der Atomhülle kann nicht jede beliebige Energie haben, sonder
für ein Elektron der Atomhülle sind nur ganz bestimmte Energieniveaus erlaubt.
Daraus ergibt sich zwangsläufig auch eine einschränkende Bedingung für die Änderung der Energie eines Elektrons im Atom:
Ein Elektron in der Atomhülle kann seine Energie nicht nach Belieben ändern.
Die vier Niveaus in Abb. 2 stellen einige der erlaubten Energiezustände in der Elektronenhülle dar, und wenn man voraussetzt, daß sich zwischen diesen eingezeichneten Niveaus keine weiteren erlaubten Engergieniveaus befinden, kann man sagen:
Ein Elektron, das sich auf Niveau 1 befindet, kann keinen Energiebetrag aufnehmen, der kleiner ist als die Engeriedifferenz zwischen Niveau 1 und 2, denn zwischen diesen beiden Niveaus darf es sich nicht aufhalten.
Die Energieportion, die ein Elektron aufnehmen oder abgeben muß, um ein anderes Energieniveau zu erreichen, wird als Energiequant bezeichnet.
Ein Elektron der Atomhülle kann sich auf der Energieskala sozusagen nur in Sprüngen aufwärts oder abwärts bewegen. Bei jedem Sprung zu einem höheren Energieniveau nimmt es ein Energiequant auf, bei jedem Sprung zu einem tieferen Energieniveau gibt es ein Energiequant ab. Die Tatsache, daß ein Elektron in der Atomhülle seine Energie nicht beliebig ändern kann, wird auch als Energiequantelung bezeichnet. Das Überwechseln eines Elektrons von einem Energieniveau auf ein anderes - in de Fachsprache als Elekronenübergang bezeichnet - läßt sich anschaulich durch Pfeile darstellen, die man in ein Energieniveauschema einzeichnet.
In Abb. 3 sind die Übergänge eines Elektrons der 1. Schale in drei energiereichere Schalen auf diese Weise dargestellt. Die Länge der Pfeile ist ein Maß für die Größe der Energiequanten, die das Elektron dabei aufnehmen muß.
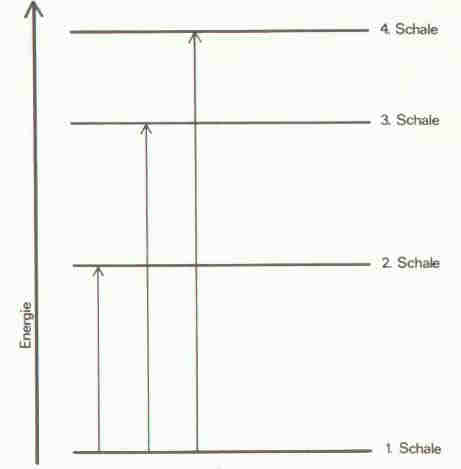 Abb.
3: Enegieniveauschema mit Elektronenübergängen
Abb.
3: Enegieniveauschema mit Elektronenübergängen
3.2.5. Energieunterniveaus
In Abb. 2 sind die Energieverhältnisse in der Elektronenhülle sehr vereinfacht dargestellt. Die dort eingezeichneten Energiehauptniveaus oder Schalen gliedern sich nämlich in Unterniveaus auf. Die Zahl der Unterniveaus für die einzelnen Elektronenschalen ist verschieden. In Abb. 4 ist diese Untergliederung wieder in einem Energieniveauschema dargestellt.

Abb. 4: Energieniveauschema für die Unternniveaus der ersten vier Elektronenschalen.
Die linke Hälfte der Abb. 4 ist identisch mit Abb. 2. Die dort eingezeichneten vier Schalen sind hier zur Orientierung noch einmal angegeben. Die gestrichelten Linien zwischen den beiden Abbildungshälften sollen verdeutlichen, in wieviele Engergiezustände sich jede Schale gliedert. Die Schalen sind wieder numeriert von 1 bis 4; bezeichnet man diese Nummer allgemein als n, dann gilt:
Eine Elektronenschale mit der Nummer n enthält n Unterniveaus.
Die 1. Schale hat also nur ein Unterniveau,
die zweite Schale hat zwei Unterniveaus, usw.
Abb. 4 darf nicht so verstanden werden, daß sich in der Elektronenhülle eines Atoms die Elektronen auf Haupt- und Unterniveaus verteilen wie etwa Hühner auf einer Leiter, die außer vielen dünnen Sprossen auch noch einige dicke enthält. Man kann sich die Enegiehauptniveaus vielmehr als eine Art Mittelwerte der zugehörigen Unterniveaus vorstellen. Sie bringen eine leichtere zu durchblickende Ordnung in die Vielzahl der Unterniveaus.
Ein Elektron der 2. Schale hat dementsprechend die Auswahl zwischen zwei verschiedenen Engergieniveaus, nicht etwa zwischen drei.
Ein Elektron der 4. Schale kann sich auf vier verschiedenen Energieniveaus befinden.
Die Unerniveaus werden durch die Zweierkombination von Zahlen und Kleinbuchstaben gekennzeichnet, die in Abb. 4 rechts angegeben sind. Die Zahl kennzeichnet die Schale, zu der das jeweilige Unterniveau gehört. Die Unterniveaus ein und derselben Schale werden in der Reihenfolge zunehmender Energie mit den Kleinbuchstaben s, p, d und f bezeichnet, die Elektronen, die sich auf diesen Niveaus befinden, als s-, p-, d- und f-Elektronen.
Anhand der Abb. 4 können Sie jetzt folgende Aussagen machen:
Ist nur ein Unterniveau pro Schale vorhanden, wie in der Schale mit der Kennziffer n = 1, dann ist es ein s-Niveau.
Die zweite Schale hat ein s- und ein p-Niveau;
die dritte Schale hat ein s-, ein p- und ein d-Niveau
die vierte Schale hat ein s-, ein p-, ein d- und ein f-Niveau
Ein s-Niveau findet man also in allen Schalen,
ein p-Niveau in den Schalen ab n = 2,
ein d-Niveau in den Schalen ab n = 3,
ein f-Niveau in den Schalen ab n = 4
Innerhalb einer Schale ist das energieärmste Unterniveau immer ein s-Niveau.
3.2.6. Ionisierungsgrenze und Ionisierungsenergie
Bereits in Abschnitt 3.2.1 wurde erläutert, daß man einem Elektron Energie zuführen muß, wenn man den Abstand zwischen Elektron und Atomkern vergrößern will. Die inneren Elektronenschalen sind energieärmer als die äußeren.
Dementsprechend mus man auch Energie aufwenden, um ein Elektron ganz aus der Elektronenhülle eines Atoms zu entfernen.
In Abb. 5 sind außer den schon von Abb. 2 bekannten Elektronenschalen ganz schematisch noch höher liegende Schalen angedeutet. Der Einfachheit wegen sind die Unterniveaus nicht eingezeichnet. Die gestrichelte Linie markiert die Energie, die das Elektron mindestens haben muß, wenn es das Atom verlassen will. Diese Linie wird Ionisierungsgrenze genannt.
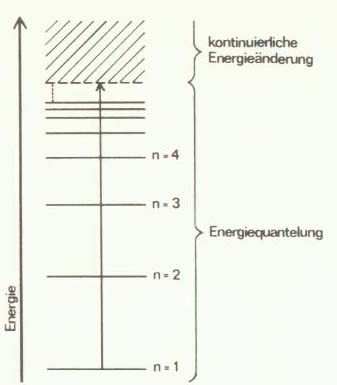 Abb.
5 Enerieniveauschema mit Ionisierungsgrenze
Abb.
5 Enerieniveauschema mit Ionisierungsgrenze
Erklärung des Namens:
Entfernt man aus einem neutralen Atom ein Elektron, dann erhält man ein Atom, das in seiner Hülle ein Elektron weniger besitzt, als seiner Kernladungszahl entspricht: folglich ist es insgesamt positiv geladen. Ein positiv oder negativ geladenes Teilchen nennt man Ion.
Ein positives Ion kann man also erhalten, wenn man einem Elektron in der Elektronenhülle eines Atoms so viel Energie zuführt, daß es die in Abb. 5 als gestrichelte Linie eingezeichnete Ionisierungsgrenze überschreiten und damit das Atom verlassen kann.
Ein Elektron oberhalb der Ionisierungsgrenze oder, was das gleiche bedeutet, außerhalb des Atoms wird als "freies Elektron" bezeichnet. Ein "freies Elektron" ist nicht mehr der Energiequantelung der Elektronenhülle unterworfen, es kann jeden beliebigen Energiebetrag aufnehmen oder, wie man häufiger sagt, es kann seine Energie kontinuierlich ändern.
Für ein Elektron, das sich beispielsweise auf dem untersten Energieniveau von Abb. 5 befindet, bedeutet das: Solange ihm Energiebeträge angeboten werden, die kleiner sind als der Pfeil in Abb. 5, muß es immer auf ein passendes Energiequant warten, das gerade groß genug ist, um irgend eines der anderen Energieniveaus in der Elektronenhülle zu erreichen. Sobald der zur Verfügung stehende Energiebetrag aber gleich groß oder größer ist als der Pfeil, kann das Elektron alles nehmen, was ihm angeboten wird, und das Atom verlassen.
Nach der Erklärung der Ionisierungsgrenze ergibt sich die Definition der Ionisierungsenergie fast von selbst:
Die Energie, die man mindestens aufwenden muß, um ein Elektron aus der Elekronenhülle eines Atoms zu entfernen, wird als Ionisierungsenergie bezeichnet.
Der Name kommt, wie bereits bei der Besprechung der Ionisierungsgrenze dargelegt wurde, daher, daß bei der Abtrennung eines Elektrons aus einem Atom ein positives Ion entsteht.
Wird bei der Ionisierung eines Atoms z. B. ein Elektron aus der 1. Schale entfernt, dann entspricht die Ionisierungsenergie dem in Abb. 5 eingezeichneten Pfeil zwischen dem Energieniveau n = 1 und der Ionisierungsgrenze.
Ausführlicher wird die Ionisierungsenerie unter dem Verzeichnis "Periodensystem" besprochen.
Zusammenfassung des Abschnitts 3.2:
Ein Elektron der Atomhülle kann seine Energie nicht kontinuierlich ändern; es unterliegt der Energiequantelung.
Die für ein Elektron erlaubten Energieniveaus und die Elektronenübergänge zwischen diesen Niveaus lassen sich übersichtlich in einem Energieniveauschema der Elektronenhülle darstellen.
Die Elekronenhülle ist in Schalen unterschiedlicher Energie gegliedert; jede Schale enthält Energieunterniveaus, deren Anzahl mit der Nummer der Schale wächst. Die Unterniveaus weden als s- , p-, d- und f-Niveaus bezeichnet.
Je energiereicher ein Elektron der Atomhülle ist, desto größer ist auch sein Abstand zum Atomkern. Um aus einem Atom ein Elektron zu entfernen, muß ein Mindestbetrag an Energie, die Ionisierungsenergie, aufgewendet werden.
In einem Energieniveauschema der Elektronenhülle markiert die Ionisierungsgrenze die Energie, die ein Elektron haben muß, um das Atom verlassen zu können.
3.3. Räumliche Anordnung der Elektronen
3.3.1 Orbitale
Über den Aufenthaltsort eines Elektrons im Atom können prinzipiell keine genauen Angaben gemacht werden. Es ist nicht möglich, etwa die genaue Bahn eines Elektrons um den Atomkern anzugeben. Man kann aber sagen, mit welcher Wahrscheinlichkeit sich das Elektron zu einer bestimmten Zeit an einem bestimmten Ort in der Umgebung des Atomkerns befindet.
Durch solche Wahrscheinlichkeitsbetrachtungen lassen sich in der Elektronenhülle Räume angeben, in denen sich die Elektronen mit sehr hoher Wahrscheinlichkeit aufhalten; diese Räume werden Orbitale genannt. Mit etws anderen Worten formuliert:
Ein Orbital ist ein Raum in der Atomhülle, in dem die Aufenthaltswahrscheinlichkeit eines Elektrons einen endlichen, d. h. von Null verschiedenen Wert hat.
Bildlich kann man sich ein Orbital vorstellen als eine mit zu langer Belichtungszeit aufgenommene unscharfe Photographie eines Elektrons. Das Elektron bewegt sich in der Atomhülle überaus schnell, so daß man die Bewegung im einzelnen nicht erfassen kann. Man "sieht" nur eine Wolke negativer elektrischer Ladung.
Man kann auch an ein Windrad denken. Wenn es sich dreht, kann man nicht die Bewegung der einzelnen Flügel verfolgen, sondern man sieht eine runde Scheibe. Bei einem Orbital hat man es allerdings nicht wie beim Windrad mit einem zweidimensionalen Gebilde zu tun, sondern mit einem dreidimensionalen.
Ein Orbital kann man sich als Ladungswolke vorstellen.
Mit dem Bild der Ladungswolke läßt sich auch der Begriff Elektronendichte recht gut verdeutlichen: Die Ladungswolke erscheint dort besonders dicht, wo die Wahrscheinlichkeit, ein Elektron anzutreffen, besonders groß ist. "Elektronendichte" u."Aufenthaltswahrscheinlichkeit" des Elektrons" werden etwa im gleichen Sinn verwendet.
Dementsprechend kann man ein Orbital entweder wie oben umschreiben als Raum, in dem die Aufenthaltswahrscheinlichkeit eines Elektrons einen endlichen Wert hat oder, gleichbedeutend damit, als Raum, in dem die Elektronendichte einen endlichen Wert hat.
Wenn man sich ein Orbital als Ladungswolke vorstellen will, muß man wissen, welche Form diese Wolke hat. Die von den Elektronen der Atomhülle gebildeten Orbitale sehen nicht alle gleich aus, sondern die Form der Orbitale ist unterschiedlich, je nach der Energie des zugehörigen Elektrons.
Den verschiedenen Energieniveaus der Elektronenhülle entsprechen verschieden geformte Orbitale.
Von dem Energieniveau erhalten wie die Elektronen auch die zugehörigen Orbitale ihren Namen. Ein Elektron auf dem 1s-Energieniveau heißt 1s-Elektron, das zugehörige Orbital heißt 1s-Orbital. Entsprechend gibt es ein 2s-Orbital, 2p-Orbital, usw.
3.3.2. s-Orbitale
Das energieärmste Energieniveau der Elektronenhülle ist das 1s-Niveau; das zugehörige 1s-Orbital ist in Abb. 6 in ein rechtwinkeliges Koordinatensystem eingezeichnet.
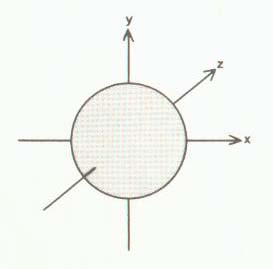 Abb.
6 1s-Orbita
Abb.
6 1s-Orbita
 2s-Orbital
2s-Orbital
Das 1s-Orbital ist kugelförmig, der Atomkern befindet sich im Ursprung des Koordinatensystems, also im Mittelpunkt des Orbitals. Vom Kern aus gesehen, gibt es im 1s-Orbital keine Richtung, in der sich das Elektron bevorzugt aufhalten würde, d. h. die Elektronendichte im 1s-Orbital ist unabhängig von der Raumrichtung. Ganz gleich um welchen Winkel man das Orbital dreht, immer erhält man das gleiche Bild. Mit anderen Worten:
Das 1s-Orbital ist kugelsymmetrisch.
Sie haben vielleicht für dieses kugelförmige Orbital die kugelsymmetrische Verteilung der Elektronendichte als Selbstverständlichkeit betrachtet. Die Richtungsunabhängigkeit der Elektronendichte wird hier deshalb so betont, weil sie im Vergleich zu anderen Orbitalen ein wesentliches Merkmal der 1s-Orbitale ist.
In Abb. 6 ist das 1s-Orbital sehr vereinfacht als Kugel dargestellt, die nach außen scharf begrenzt ist. Aufgrund dieser Darstellung ist es vielleicht auch naheliegend anzunehmen, daß sich das Elektron im Inneren dieser Kugel überall mit der gleichen Wahrscheinlichkeit aufhalten kann. Diese Vorstellungen sind falsch.
Ein Orbital hat nach außen keine scharfe Grenze. Die Elektronendichte ändert sich mit dem Abstand vom Atomkern.
Abb. 7 zeigt eine Möglichkeit, die Elektronendichteverteilung im 1s-Orbital anschaulich darzustellen.

Abb. 7: Querschnitt durch ein 1s-Orbital mit Atomkern (die Schnittebene geht durch den Atomkern)
Man kann Abb. 7 interpretieren als Querschnitt durch die einem 1s-Elektron entsprechende Ladungswolke. Der Atomkern ist zur besseren Orientierung in der Mitte eingezeichnet.
Die dem 1s-Elektron entsprechende Ladungswolke hat ihre größte Dichte in der Nähe des Atomkerns, nach außen nimmt die Dichte ständig ab.
Man kann sich Abb. 7 entstanden denken durch ein Übereinanderprojizieren sehr vieler Momentaufnahmen eines 1s-Elektrons. Bei jeder Aufnahme wird der momentane Aufenthaltsort des Elektrons festgestellt. Jeder Punkt entspricht also einer Aufnahme. In der Nähe des Kerns, wo die Punkte sehr dicht liegen, ist die Aufenthaltswahrscheinlichkeit des 1s-Elektrons am größten. Mit zunehmendem Abstand vom Atomkern wird die Aufenthaltswahrscheinlichkeit immer kleiner.
Auch in noch größerer Entfernung vom Kern als in Abb. 7 besteht eine gewisse, wenn auch sehr kleine, Wahrscheinlichkeit, das Elektron zu finden. Absolut Null wird die Aufenthaltswahrscheinlichkeit eines Elektrons sogar erst im Unendlichen.
Nicht nur das 1s-Orbital, sondern alle Orbitale erstrecken sich streng genommen bis ins Unendliche. Mit unendlich großen Orbitalen kann man in der Praxis wenig anfangen, man kann sie vor allem nicht zeichnen. Auch die Darstellungsweise von Abb. 7 ist für den alltäglichen Gebrauch zu aufwendig. Man hat sich deshalb geeinigt, Orbitale wie das 1s-Orbital in Abb. 6 mit einer scharfen Grenze zu zeichnen. Diese Grenze ist immer so gewählt, daß sie Orte gleicher Aufenthaltswahrscheinlichkeit des Elektrons miteinander verbindet und daß sie einen Raum umschließt, der das Elektron mit etwa 90 % Wahrscheinlichkeit enthält.
Zur Diskussion alltäglicher chemischer Probleme sind die auf diese Art gezeichneten Orbitale bei weitem genau genug, und näherungsweise kann man durchaus sagen, daß die Elektronendichte außerhalb eines solchen Orbitals gleich Null ist. Die Änderung der Elektronendichte in Abhängigkeit vom Kernabstand, die durch Abb. 7 recht anschaulich wiedergegeben wird kann man auch wie in Abb. 8 graphisch darstellen.

Abb. 8: Aufenthaltswahrscheinlichkeit des 1s-Elektrons pro Volumenelement in Abhängigkeit vom Kernabstand.
Man denkt sich, vom Atomkern ausgehend, eine Gerade durch das 1s-Orbital nach außen gelegt. Auf der Geraden sollen viele kleine Volumenelemente, alle von der gleichen Größe, aneinandergereiht sein. Bestimmt man nun in jedem dieser Volumenelemente die Wahrscheinlichkeit, mit der das Elektron darin anzutreffen ist, und trägt diesen Wert gegen den Abstand des Volumenelements vom Atomkern auf, dann ergibt sich die Kurve von Abb. 8.
Diese Kurve zeigt in Übereinstimmung mit Abb. 7: Die Aufenthaltswahrscheinlichkeit des 1s-Elektrons in einem Volumenelement ist in der Nähe des Kerns am größten, sie wird mit zunehmender Entfernung vom Kern immer kleiner; den Wert Null erreicht die Kurve erst im Unendlichen.
Eine zusätzliche Information über die Elektronendichteverteilung im 1s-Orbital kann man aus der in Abb. 9 gezeigten graphischen Darstellung erhalten. Man denkt sich das 1s-Orbital aufgeteilt in viele Kugelschalen von geringer Dicke, die alle konzentrisch um den Atomkern angeordnet sind. Bestimmt man dann in jeder dieser Kugelschalen die Aufenthaltswahrscheinlichkeit des Elektrons und trägt sie gegen den Abstand der Kugelschale vom Atomkern auf, dann erhält man die Kurve der Abb. 9.

Abb. 9: Aufenthaltswahrscheinlichkeit des 1s-Elektrons pro Kugelschale in Abhängigkeit vom Kernabstand
Diese Kurve hat anders als die Kurve von Abb. 8 in der Nähe des Atomkerns sehr kleine Werte, dann steigt sie rasch zu einem Maximum an und fällt langsam wieder ab, bis sie im Unendlichen den Wert Null erreicht. Aufgrund des Kurvenverlaufs von Abb. 9 kann man sagen:
In der dem 1s-Elektron entsprechenden Ladungswolke gibt es eine Kugelschale, in der die Elektronendichte größer ist als in jeder anderen Schale.
Woher kommt der Unterschied zwischen den beiden Kurven in den Abbildungen 8 und 9?
In Kernnähe ist zwar die Aufenthaltswahrscheinlichkeit des Elektrons pro Volumenelement am größten, dort ist jedoch das Volumen einer Kugelschale sehr klein, d.h. sie enthält sehr viel weniger Volumenelemente als eine Kugelschale in größerem Abstand vom Kern. Auf diese Weise ergibt sich ein Maximum für einen Kugelradius, bei dem die Kugelschale eine genügend große Zahl von Volumenelementen enthält und jedes dieser Volumenelemente noch eine ziemlich große Aufenthaltswahrscheinlichkeit des Elektrons aufweist.
Ein s-Energieniveau gibt es nicht nur in der innersten Elektronenschale.- Erinnern Sie sich? Ein s-Unterniveau gibt es in allen Elektronenschalen ( vgl. Abschnitt 3.2.5 ) - Wie sehen die Orbitale aus, die diesen energiereicheren s-Energieniveaus entsprechen?
Alle s-Orbitale der Elektronenhülle sind kugelsymmetrisch, d. h. vom Atomkern aus betrachtet, ist die Aufenthaltswahrscheinlichkeit aller s-Elektronen in allen Raumrichtungen gleich groß.
Etwas anders als beim 1s-Orbital ist in den energiereicheren s-Orbitalen die Elektronendichte bei verschiedenen Kernabständen verteilt. Für das 2s-Orbital ist in Abb. 10 die Aufenthaltswahrscheinlichkeit des Elektrons pro Kugelschale in Abhängigkeit vom Kernabstand graphisch dargestellt. Vergleichen Sie den Kurvenverlauf mit dem vom Abb. 9. Auf zwei wesentliche Unterschiede soll etwas näher eingegangen werden.
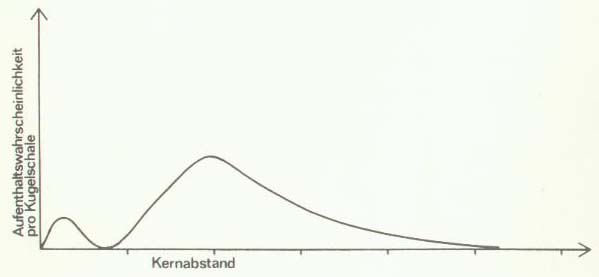
Abb. 10: Aufenthaltswahrscheinlichkeit des 2s-Elektrons pro Kugelschale in Abhängigkeit vom Kernabstand
1) Das große Maximum der Kurve von Abb. 10 liegt bei größerem Kernabstand als das Maximum in Abb. 9; das heißt, ganze einfach ausgedrückt, das 2s-Orbital ist größer als das 1s-Orbital. Etwas genauer formuliert: Das 2s-Orbial hat seine größte Elektronendichte in einer Kugelschale, die einen größeren Radius besitzt als die entsprechende Kugelschale des 1s-Orbitals. Mit noch etwas anderen Worten:
Das 2s-Elektron hält sich mit der höchsten Wahrscheinlichkeit in einem größeren Abstand vom Atomkern auf als das 1s-Elektron.
Abb. 10 zeigt aber auch deutlich, daß sich das 2s-Elektron mit einer gewissen Wahrscheinlichkeit auch sehr nahe am Kern aufhalten kann. Es ist also nicht so, daß sich das 2s-Elektron immer in größerem Abstand vom Atomkern aufhält als das 1s-Elektron. Seine Aufenthalts- wahrscheinlichkeit in größerer Entfernung ist nur wesentlich höher als die nahe am Kern.
Die größere Entfernung des 2s-Elektrons vom Atomkern entspricht seinem höheren Energieinhalt. - Erinnern Sie sich? Um ein Elektron in einen größeren Abstand vom Atomkern zu bringen, muß dem Elektron Energie zugeführt weden.( Vgl. Abschnitt 3.2.1 )
2) Die Aufenthaltswahrscheinlichkeit des 2s-Elektrons pro Kugelschale steigt, vom Kern ausgehend, zunächst an, fällt dann aber, anders als beim 1s-Elektron, auf Null zurück, bevor sie den höchsten Wert erreicht. Das bedeutet: Im 2s-Orbital gibt es eine Kugelfläche, in der sich das Elektron nie aufhält. Eine Fläche oder Ebene in einem Orbital, in der die Aufenthaltswahrscheinlichkeit des Elektrons gleich Null ist, wird als "Knotenfläche" oder " Knotenebene" bezeichnet.
Das 2s-Orbital hat eine kugelförmige Knotenfläche.
Man kann sich das 2s-Orbital dementsprechend etwa vorstellen wie eine Hohlkugel, die im Inneren noch eine kleine Kugel enthält.
Zusammenfassend kann man für die s-Orbitale der Elektronenhülle sagen:
Alle s-Orbitale sind kugelsymmetrisch. Mit zunehmender Energie der s-Elektronen wird der Durchmesser der zugehörigen Orbitale größer, ebenso nimmt die Zahl der Knotenflächen zu. Das 1s-Orbital hat keine Knotenfläche.
Von außen gesehen unterscheiden sich die verschiedenen s-Orbitale nur durch ihre Größe; Abb. 6 kann deshalb ganz allgemein als Darstellung eines s-Orbitals betrachtet werden, nicht nur als Darstellung des 1s-Orbitals.
3.3.3. p-Orbitale
Bei den p-Energieniveaus tritt im Vergleich zu den s-Energieniveaus eine Besonderheit auf. Ein Elektron, das sich auf einem p-Energieniveau befindet, hat die Wahl zwischen drei verschiedenen p-Orbitalen.
Zu jedem p-Energieniveau gehören drei p-Orbitale.
Das energieärmste p-Energieniveau liegt in der zweiten Elektronenschale. Die drei zugehörigen 2p-Orbitale sind in Abb. 11 jeweils in einem rechtwinkligen Koordinatensystem dargestellt.
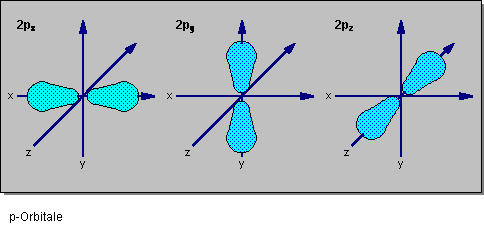
Abb. 11: Form und räumliche Orientierung der drei 2p-Orbitale.
Die drei 2p-Orbitale haben alle die gleiche Form: Sie sind hantelförmig; der Atomkern befindet sich im Schnittpunkt der beiden Hantelhälften.
Bei einem 2p-Orbital ist also im Gegensatz zu einem s-Orbital die Elektronendichte nicht kugelsymmetrisch um den Atomkern verteilt. vom Atomkern aus gesehen, gibt es eine Richtung im Raum, in der sich ein 2p-Elektron bevorzugt aufhält.
Ein 2p-Orbital besitzt eine Vorzugsrichtung im Raum.
Die drei 2p-Orbitale sind entlang den Achsen eines rechtwinkligen Koordinatensystems ausgerichtet mit dem Schnittpunkt der Hantelhälften im Koordinatenursprung. Entsprechend ihrer räumlichen Orientierung werden sie benannt: Das 2px-Orbital beispielsweise erstreckt sich entlang der x-Achse, das dazu senkrecht längs der z-Achse ausgerichtete 2p-Orbital wird als 2pz-Orbital bezeichnet.
Die drei 2p-Orbitale unterscheiden sich nur durch ihre räumliche Orientierung. Sie sind senkrecht zueinander ausgerichtet.
Dreht man ein 2p-Orbital um seine Längsachse um beliebige Winkel, dann erhält man immer das gleiche Bild des Orbitals, wenn man in Richtung der Drehachse blickt, das heißt:
Ein 2p-Orbital ist rotationssymmetrisch bezüglich seiner Längsachse.
Das 2px-Orbital z. B. ist rotationssymmetrisch bezüglich der x-Achse.
Die Rotationssymmetrie betrifft natürlich nicht nur die in Abb. 11 dargestellte äußere Form der 2p-Orbitale, sondern sie bezieht sich ganz allgemein auf die Verteilung der Elektronendichte im Orbital. Bereits im Abschnitt 3.2.2 wurde am Beispiel des 1s-Orbitals recht ausführlich dargelegt, daß die Elektronendichte im Orbital nicht einheitlich ist. Auf die Änderung der Elektronendichte in einem 2p-Orbital soll hier nur kurz eingegangen werden: Sie ändert sich sowohl entlang der Längsachse als auch senkrecht zur Längsachse. Etwa in der Mitte der beiden Hantelhälften ist sie am größten und nimmt nach außen allmählich ab.
Dabei bedeutet Rotationssymmetrie der Elektronendichte bezüglich der Längsachse des Orbitals z. B. für das 2px-Orbital: Schneidet man das 2px-Orbital senkrecht zur x-Achse in Scheiben, dann findet man in einer solchen Scheibe in einem bestimmten Abstand vom Scheiben- mittelpunkt überall die gleiche Elektronendichte.
Die Elektronendichte eines 2p-Orbitals ist im Schnittpunkt der beiden Hantelhälften gleich Null. Sie ist sogar nicht nur an diesem Punkt Null, sondern in der ganzen Ebene, die senkrecht auf der Längsachse des Orbitals durch den Schnittpunkt der beiden Hantlhälften verläuft. - Erinnern Sie sich? Eine Ebene in einem Orbital, in der die Aufenthaltswahrscheinlichkeit des Elektrons gleich Null ist, wird Knotenebene genannt. ( Vgl. 3.3.2 )
Die 2p-Orbitale besitzen eine Knotenebene.
Die Knotenebene des 2px-Orbitals ist die yz-Ebene, die Knotenebene des 2py-Orbitals ist die xz-Ebene.
Noch eine Bemerkung zu Abb. 11
Bei der Besprechung des 1s-Orbitals wurde bereits mit Gültigkeit für alle Orbitale betont, daß die scharfe Grenze der üblichen Orbitalbilder nur als Vereinfachung aus praktischen Gründen zu betrachten ist. Tatsächlich stellt jedes Orbital eine Ladungswolke mit unscharfer äußerer Grenze dar.
Dementprechend ist auch die Darstellung der Orbitale in Abb. 11 zu verstehen. Wie bereits erwähnt, beträgt die Wahrscheinlichkeit, das Elektron innerhalb der eingezeichneten Grenzen eines solchen Orbitals zu finden , etwa 90 %.
Auf die p-Orbitale der energiereicheren Elektronenschalen soll nur kurz eingegangen werden:
Es gibt wie in der 2. Elektronenschale jeweils drei energiegleiche p-Orbitale in einer Schale. Die drei p-Orbitale einer Schale haben die gleiche Form. Die Form der energiereicheren p-Orbitale ist nicht mehr ganz so einfach wie die der 2p-Orbitale, da innerhalb der Orbitalhälften Knotenflächen dazukommen. Aber näherungsweise kann man auch die energiereicheren p-Orbitale als Hantel bezeichnen. Alle p-Orbitale sind wie die 2p-Orbitale bezüglich ihrer Längsachse rotationssymmetrisch und haben im Schnittpunkt der Hantelhälften senkrecht zur Längsachse eine Knotenebene. Entsprechend dem höheren Energieinhalt erreicht in den p-Orbitalen der höheren Elektronenschalen die Elektronendichte erst bei einem größeren Kernabstand ihr Maximum, d. h. diese p-Orbitale sind größer als die 2p-Orbitale.Die drei p-Orbitale einer Schale sind wie die 2p-Orbitale senkrecht zueinander ausgerichtet. Entsprechend ihrer Orientierung werden sie jeweils als px, py und pz-Orbital bezeichnet. Näherungsweise kann man also auch die energiereicheren p-Orbitale wie die 2p-Orbitale in Abb. 11 darstellen.
3.3.4. d- und f-Orbitale
Aus Abb. 4 ist zu entnehmen, daß es in den höheren Elektronenschalen außer s- und p-Energieniveaus auch d-Niveaus ( ab n = 3 )und f-Niveaus ( ab n = 4 ) gibt.
Zu einem d-Energieniveau gehören fünf d-Orbitale. Zu einem f-Energieniveau gehören sieben f-Orbitale.
Die Form der d- und f-Orbitale soll hier nicht besprochen werden. Merken sollten Sie sich nur:
d- und f-Orbitale haben Vorzugsrichtungen im Raum.
Die kugelsymmetrische Verteilung der Elektronendichte ist also tatsächlich eine Besonderheit der s-Orbitale.
3.4. Kästchendarstellung der Orbitale
siehe dazu auch: 1. Darstellung des Energieniveauschemas
In den vorhergehenden Abschnitten war zunächst von den Energieniveaus der Elektronenhülle die Rede, dann von der Form und der Zahl der Orbitale, die diesen Energieniveaus entsprechen.
In Abb. 12 sind nun Zahl und Energie der Orbitale für die vier untersten Elektronenschalen in einer recht anschaulichen Weise mit Hilfe von Kästchen dargestellt, die auf einer Energieskala angeordnet sind.
Jedes Kästchen entspricht einem Orbital.
Orbitale der gleichen Art werden meist als Block gezeichnet, z. B. die p-Orbitale als Dreierblock.

Abb. 12: Energieniveauschema der ersten vier Elektronenschalen mit Kästchendarstellung der Orbitale
Abb. 12 ist nichts anderes als ein Energieniveauschema, in dem die Energieniveaus aber nicht wie bisher durch Sriche, sondern durch Kästchen angegeben sind. Zu Ihrer Orientierung ist links in der Abbildung das Energieniveauschema eingezeichnet, das Sie schon von Abb. 4 kennen. In der Kästchendarstellung sind die Unterniveaus einer Schale nicht mehr übereinander in einer Spalte angeordnet, sondern sie sind seitlich versetzt, so daß jeweils die s- , p- und d-Niveaus der verschiedenen Schalen untereinander stehen. Diese seitliche Verschiebung dient ausschließlich der besseren Übersicht, denn in einem Energieniveauschema hat die Abszisse keine physikalische Bedeutung.
Um in Abb. 12 deutlich zu machen, welche Unterniveaus jeweils zur gleichen Schale gehören, sind die Schalen abwechselnd schraffiert und nicht schraffiert.
Der Kästchendarstellung von Abb. 12 lassen sich sehr einfach einige Informationen entnehmen, die Ihnen bereits von früheren Abschnitten bekannt sind:
In jeder Elektronenschale kommt mit steigender Nummer ein neuer Block von Orbitalen dazu. In der ersten Schale gibt es nur ein s-Orbital; in der zweiten Schale kommen die p-Orbitale dazu, in der dritten Schale die d-Orbitale, in der vierten Schale die f-Orbitale. Innerhalb einer Schale steigt die Zahl der Orbitale pro Unterniveau mit zunehmender Energie dieser Unterniveaus immer um zwei: Es gibt ein s-Orbital, drei p-Orbitale, fünf d-Orbitale, sieben f-Orbitale.
3.5. Verteilung der Elektronen auf die Orbitale
Die Kästchendarstellung bietet eine Möglichkeit, Zahl und Energie der Orbitale in der Elektronenhülle von Atomen übersichtlich darzustellen. Wie verteilen sich nun die Elektronen auf diese Orbitale?
3.5.1. Maximale Elektronenzahl pro Orbital
Zunächst muß man ein wichtiges Prinzip kennen, das nach seinem Entdecker PAULI - Prinzip genannt wird:
In einem Orbital können sich nie mehr als zwei Elektronen befinden.
Aufgrund dieses Prinzips gibt es innerhalb einer Elektronenschale also maximal zwei s-Elektronen, sechs p-Elektronen und zehn d-Elektronen.
Sie können jetzt auch anhand der Abb. 12 durch einfaches Abzählen feststellen, wieviele Elektronen maximal in den einzelnen Elektronenschalen Platz finden.
| Schalennummer | n = 1 | n = 2 | n = 3 | n = 4 |
| Maximale Elektronenzahl pro Schale | 2 | 8 | 18 | 32 |
Als Formel ausgedrückt, ist die maximale Elektronenzahl einer Schale gleich 2n2, wenn n die Nummer der Schale ist. Sie brauchen sich weder diese Formel noch die Zahlen der Tabelle zu merken. Es ist nützlicher, wenn Sie Art und Zahl der Orbitale für jede Schale im Gedächtnis behalten; mit dem PAULI - Prinzip ergibt sich dann die maximale Zahl der Elektronen pro Schale von selbst.
Anmerkung:
Vielleicht haben Sie sich daran gestört, daß im Vorangehenden von den Orbitalen gesprochen wurde, als seien sie leerstehende Plätze in der Elektronenhülle, die von Elektronen besetzt werden können, obwohl streng genommen entsprechend der Definition eines Orbitals als Ladungswolke oder als Raum endlicher Elektronendichte ein Orbital gar nicht existiert, wenn kein Elektron vorhanden ist.
Es ist aber üblich, auch von " leeren Orbitalen " oder von " unbesetzten Orbitalen " zu sprechen, weil es bei vielen Überlegungen sehr nützlich ist, auch die Räume in der Elektronenhülle zu berücksichtigen, in denen sich in einem speziellen Fall vielleicht noch keine Elektronen aufhalten, die aber von Elektronen eingenommen werden können.
3.5.2. Reihenfolge beim Besetzen der Orbitale
Bis jetzt war immer die Rede von der maximal möglichen Zahl der Elektronen in einem Orbital oder einer Elektronenschale. Wie verteilt sich aber eine gegebene Zahl von Elektronen auf die vorhandenen Plätze in der Elektronenhülle?
Die von den Elektronen begehrtesten Plätze sind die energieärmsten, das bedeutet:
Die Orbitale, die auf der Energieskala am weitesten unten stehen, werden zuerst besetzt.
Damit läßt sich für jedes beliebiges Element sehr einfach die Elektronenverteilung konstruieren:
Man zeichnet sich in der Kästchenschreibweise ein Energieniveauschema der Elektronenhülle auf. Dann schüttet man gleichsam von oben die für das betrachtete Element charakteristische Elektronenzahl in das Schema hinein. - Erinnern Sie sich? Elektronenzahl = Ordnungszahl oder Kernladungszahl des Elements. - Die Elektronen füllen dann die Orbitale von unten nach oben auf.
Entsprechend diesem Aufbauprinzip befindet sich das Elektron des Wasserstoffatoms mit der Ordnungszahl 1 im 1s-Orbital ( Vgl. Abb. 12 ). Das Element mit der Ordnungszahl 2, das Helium, bringt seine beiden Elektronen auch im 1s-Orbital unter, dann ist dieses Orbital voll besetzt. Das Element Lithium mit der Ordnungszahl 3 muß sein drittes Elektron im energetischen höher liegenden 2s-Orbital ansiedeln.
Für Lithium ist die Elektronenverteilung im Energieniveauschema Abb. 14 eingezeichnet. Jedes Elektron ist durch einen Punkt dargestellt.

Wenn Sie die HUNDsche Regel noch nicht kennen, haben Sie beim Kohlenstoff sicher gezögert, in welches der drei 2p-Orbitale Sie das sechste Elektron einfüllen sollen. Die HUNDsche Regel besagt:
Bei energiegleichen Orbitalen, z. B. den drei 2p-Orbitalen, wird jedes Orbital zuerst nur mit einem Elektron besetzt. Erst nachdem alle energiegleichen Orbitale einfach besetzt sind, kommt in jedes Orbital noch ein zweites Elektron.
Mit dieser Regel läßt sich die Elektronenhülle aller Elemente nun wirklich problemlos aufbauen.
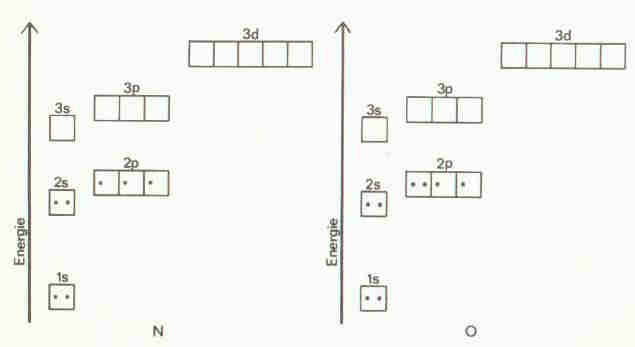
Abb. 15: Elektronenverteilung für die Elemente Stickstoff ( N ) und Sauerstoff ( O ).
Die Elektronenverteilung auf die verschiedenen Orbitale bezeichnet man auch als: Elektronenkonfiguration. Die Abbildung 14 und 15 stellen also die Elektronenkonfiguration verschiedener Elemente dar.
Noch einmal zur Wiederholung das Verfahren, mit dem sich die Elektronenkonfiguration eines bestimmten Elements herleiten läßt:
Die Ordnungszahl und damit die Elektronenzahl des Elements muß bekannt sein.
Man zeichnet sich ein Energieniveauschema der Orbitale in der Kästchenschreibweise.
Man füllt die Elektronen in das Schema ein, dabei ist zu beachten:
- Die energieärmsten Orbitale werden zuerst besetzt.
- In jedem Orbital haben maximal zwei Elektronen Platz ( PAULI - Prinzip )
- Energiegleiche Orbitale werden zunächst einfach besetzt ( HUNDsche Regel )
3.6. Spin der Elektronen
In den Abbildungen 14 und 15 wurde bei doppelt besetzten Orbitalen kein Unterschied zwischen den beiden Elektronen gemacht. Beide wurden einheitlich durch einen Punkt dargestellt. Diese Darstellung war etwas vereinfacht, denn man schreibt den Elektronen einen sogenannten Spin zu.
Das englische " to spin " heißt auf deutsch " sich drehen " . Wenn man sich vorstellt, daß sich ein Elektron rechts herum oder links herum drehen kann, wird verständlich, daß der Spin eine Eigenschaft darstellt, durch die sich zwei Elektronen unterscheiden können.
Berücksichtigt man den Spin der Elektronen, dann muß das PAULI - Prinzip schärfer formuliert werden:
In jedem Orbital können sich maximal zwei Elektronen aufhalten, die sich durch ihren Spin unterscheiden müssen.
Will man die Elektronenkonfiguration eines Elements unter Berücksichtigung des Spins darstellen, dann zeichnet man die Elektronen nicht als Punkte, sondern als kleine Pfeile, welche die unterschiedliche Spinrichtung andeuten sollen. In Abb. 16 ist die Elektronenkonfiguration des Elements Kohlenstoff in dieser Schreibweise angegeben.
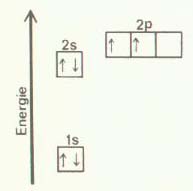 Abb.
16: Elektronenkonfiguration des Elements Kohlenstoff.
Abb.
16: Elektronenkonfiguration des Elements Kohlenstoff.
Bei doppelt besetzten Orbitalen müssen die beiden Elektronen also immer einen entgegengesetzten Spin haben, dargestellt durch die in verschiedene Richtungen zeigenden Pfeile. Sind mehrere einfach besetzte Orbitale vorhanden, wie in Abb. 16 die beiden 2p-Orbitale, dann ist es im allgemeinen üblich, die Pfeile in die gleiche Richtung zu orientieren.
3.7. Quantenzahlen
Opische Darstellung der Quantenzahlen
In den vorhergehenden Abschnitten ist die Struktur der Elektronenhülle beschrieben worden. Die Elektronen eines Atoms verteilen sich auf verschiedene Energieniveaus, auf unterschiedliche Orbitale, und sie können sich noch durch ihren Spin unterscheiden.
Daraus ergibt sich, daß man vier Kenngrößen braucht, um ein bestimmtes Elektron der Elektronenhülle eindeutig bezeichnen zu können:
Erste Kenngröße: Hauptquantenzahl n
- Die Hauptquantenzahl entspricht der jeweiligen Bohrschen Bahn n. Sie kann nur ganzzahlige Werte annehmen: n = 1, 2, 3, 4... oder einfacher : Nummer der Elektronenschale.
Zweite Kenngröße: Bahndrehimpulsquantenzahl l
- Die Bahndrehimpulsquantenzahl bestimmt die räumliche Gestalt der Atomorbitale. Sie kann die Werte l = 0, 1, 2, 3...n - 1 annehmen. l muß aber stets kleiner als n sein. Beispiel: Wenn n = 3 ist, kann l nur die Werte 0, 1, 2 annehmen. oder einfacher: In jeder Elektronenschale, außer der ersten, ist eine Unterscheidung notwendig, zwischen den verschiedenen Unterniveaus, ob s-, p-, d- oder f-Niveau.
Dritte Kenngröße: Magnetische Quantenzahl m
- Die magnetische Quantenzahl beschreibt die Anzahl der Orientierungsmöglichkeiten, die ein bestimmtes Atomorbital relativ zur Richtung eines angelegten Magnetfeldes einnehmen kann.
m kann negativ und positive, ganzzahlige Werte so wie den Wert null annehmen. Die erlaubten Werte für m sind abhängig von dem Bahndrehimpuls: Quantenzahl l
m = -l, -l + 1 ... -2, -1, 0, 1, 2, ... l - 1, l.
Beispiel: Wenn l den Wert 2 hat , kann m die Werte -2, -1, 0, 1, 2 annehmen.
oder einfacher: Außer beim s-Orbital muß zwischen mehreren energiegleichen Orbitalen verschiedener räumlicher Orientierung unterschieden werden. Für die drei p-Orbitale kennen Sie diese unterschiedlichen Bezeichnungen : px-, py- und pz-Orbital.
Vierte Kenngröße: Spinquantenzahl s
- Die Spinnquantenzahl beschreibt zwei mögliche Zustände eines Elektrons, die, anschaulich gedeutet, die Rotation eines Elektrons rechts oder links um seine eigene Achse darstellen. Diese Rotation wird als Spin bezeichnet. Die Quantenzahlen für die beiden Zustände sind + 0,5 und - 0,5.
oder einfacher: Der Spin erlaubt es, zwischen den maximal zwei Elektronen eines Orbitals zu unterscheiden.
Diese vier Kenngrößen nennt man die vier Quantenzahlen eines Elektrons.
Jede Quantenzahl kann ganz bestimmte Zahlenwerte annehmen. Im folgenden sind zur Veranschaulichung einige solche Zahlenwerte aufgeführt; Sie brauchen sie nicht zu behalten. Bei der ersten Quantenzahl sind die Zahlenwerte die Nummern der Elektronenschalen, also die Zahlen 1, 2, 3 usw. Bei der zweiten Quantenzahl steht beispielsweise der Zahlenwert 0 für s-Energieniveau oder s-Orbital, 1 steht für p-Energieniveau oder p-Orbital. Die dritte Quantenzahl kann für ein p-Elektron die Zahlenwerte +1, 0 oder -1 annehmen und unterscheidet damit zwischen den drei energiegleichen verschiedenen orientierten p-Orbitalen. Die vierte Quantenzahl kann +0,5 oder -0,5 sein, je nachdem, ob sich das Elektron rechts herum oder links herum dreht.
Jedes Elektron in einem Atom läßt sich durch eine Kombination von vier Quantenzahlen eindeutig charakterisieren.
Um Sie mit dem Sinn der Quantenzahlen etwas vertrauter zu machen, soll noch ein Beispiel besprochen werden:
Was bedeuten für ein Elektron etwa die vier Quantenzahlen 2; 1; +1; -0,5 ?
Die erste Quantenzahl gibt die Nummer der Elektronenschale an. In unserem Beispiel hat die den Wert 2; das Elektron befindet sich also in der 2. Schale. Die zweite Quantenzahl kennzeichnet die Art des Unterniveaus oder Orbitals, ob s, p, d oder f. In unserem Beispiel hat sie den Wert 1. Die 1 steht für p-Orbital. Aus den ersten beiden Quantenzahlen kann man also entnehmen, dass das Elektron ein 2p-Elektron ist. Die dritte Quantenzahl unterscheidet zwischen energiegleichen Orbitalen verschiedener räumlicher Orientierung. In unserem Beispiel hat sie den Wer +1. Für die Elektronen in den beiden anderen p-Orbitalen hätte zum Unterschied davon die dritte Quantenzahl den Wert 0 oder -1. Die vierte Quantenzahl gibt den Spin des Elektrons an. In unserem Beispiel hat sie den Wert -0,5. Für das zweite Elektron im gleichen Orbital müßte die vierte Quantenzahl den Wert +0,5 haben.
Nach der Einführung der Quantenzahlen kann nun das PAULI-Prinzip in seiner allgemeinen Form gebracht werden: In der Elektronenhülle eines Atoms gibt es niemals zwei Elektronen die in allen Quantenzahlen übereinstimmen. Erinnern Sie sich noch an die Beiden früheren Formulierungen des PAULI-Prinzips? Wenn nicht, dann schauen Sie unter 3.5.1. und 3.6.
Zusammenfassung des Abschnitts 4:
Bei der Beschreibung der Elektronenhülle wurde als erstes kurz dargelegt, welche Anzahl von Elektronen ein bestimmtes Atom enthält.
Anschließend wurde recht ausführlich besprochen, auf welchen Energieniveaus sich diese Elektronen befinden können; dabei wurden unter anderem die Begriffe Energieniveauschema, Elektronenschale, Energieunterniveau, Energiequantelung und Ionisierungsenergie erläutert.
Am Beispiel der s- und p-Unterniveaus wurde dann gezeigt, dass den einzelnen Energieniveaus eine ganz bestimmte räumliche Anordnung der Elektronen entspricht. Orbital, Elektronendichte, Aufenthaltswahrscheinlichkeit, Kugel- und Rotationssymmetrie sind einige der Begriffe, die in diesem Abschnitt besprochen wurden.
Schließlich wurde die Kästchendarstellung beschrieben, die es erlaubt, Zahl und relative Energie der Orbitale übersichtlich in einem Energieniveauschema darzustellen.
Dann wurde gezeigt, wie sich für ein Bestimmtes Element die Elektronenkonfiguration herleiten läßt. PAULI-Prinzip und HUNDsche Regel sind dabei von Bedeutung.
Abschließend wurde noch der Elektronenspin eingeführt und die Quantenzahlen, die es erlauben, jedes Elektron der Elektronenhülle eindeutig zu charakterisieren.